Fast unpacking of QC bit-flags in Python

Satellite remote sensing products often represent quality control (QC) information as bit-flags, a sequence of binary digits that individually (single digit) or collectively (multiple digits) convey additional information about a remote sensing measurement. This information may be related to cloud cover, atmospheric conditions in general, the status of the space-borne sensor, or the overall quality of the retrieval. Bitflags are convenient because a sequence of varied true/ false (binary) indicators can be represented as a decimal number. Here's an example from the Moderate Resolution Imaging Spectrometer (MODIS) MOD15 product User Guide.

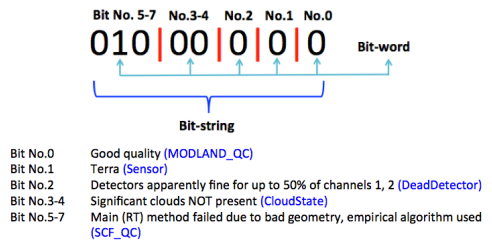
Strictly speaking, the phrase "bit-word" is misappropriated here; computer scientists have told me it refers to a sequence of two bytes (16 bits total). It may be more appropriate to refer to them as bit-flags. The example above is the binary equivalent of the decimal number 64. For a given remote sensing image, in addition to the raster array of data values (e.g., remotely sensed leaf area index, as in the MOD15 example), there is a QC band that has the same size and shape but is full of decimal values. Where the QC band has the decimal number 64, based on the above example, we can infer that the corresponding pixel in the data band has "good quality" (bit number 0) and "significant clouds [were] NOT present" (bits numbered 3-4).

Converting from Decimal to Binary Strings

The problem of trying to determine whether certain conditions apply to a given data pixel, then, is the problem of converting from decimal to binary strings. While this is relatively trivial for a single decimal number, we often need to do this conversion or "unpacking" of bit-flags for several thousands or millions of pixels at once, in the case of large or high-resolution raster image. Recently, I developed a pipeline for extracting MODIS MOD16 data in 500-m tiles (on the MODIS Sinusoidal grid), masking out low-quality pixels, resampling to 1000-m, and stitching in a global mosaic. Line profiling revealed that, by far, the most time-intensive operation was unpacking the QC bit-flags!

So, what's the fastest way to do unpack QC bit-flags in Python? Equivalently, what's the fastest way to convert from decimal to binary strings for an arbitrary array of decimal numbers? There are several options, assuming we have 8-bit binary strings that we need to unpack and parse for bit-flags. For clarity, we're evaluating options that behave something like (to use the previous example yet again):

>>> my_function(64)
'01000000'

Option 1: NumPy's Binary Representation

NumPy's binary_repr() function is a straight-forward, high-level interface for converting decimal numbers to binary strings. It's not a ufunc, however, so if we want to apply it to an arbitrary array, we need to vectorize it. In addition, we need to use partial() to curry a version of this function that always returns 8-bit binary strings. Vectorizing functions makes them slow, so I don't expect this one to perform best.

import numpy as np
from functools import partial
dec2bin_numpy = np.vectorize(partial(np.binary_repr, width = 8))

In fact, this is the approach I was originally using, which accounted for the vast majority of the program's run-time.

Option 2: Python's Built-in Binary Conversion

Python, of course, has a built-in function bin() to do this conversion. The strings returned by bin() have a special format (e.g., 0b1000000 for 64) that's not exactly what we want when unpacking QC bit-flags, so we need to use additional string methods to get a compact, 8-bit string representation. This function must also be vectorized, so it may be slow.

import numpy as np
dec2bin_py = np.vectorize(lambda v: bin(v).lstrip('0b').rjust(8, '0'))

Option 3: Bitwise Operators

A common solution for decimal-to-binary conversion in any language is the use of bitwise operators. Below, we use the left shift operator, << to get an array of decimal numbers that represent every 8-bit string with exactly one 1. Then, the bitwise AND operator & compares each of these 8 options with the (implicitly binary) representation of the decimal number we want to convert to a binary string. In effect, this updates the array with powers of 2 that, when compared to 0, are converted to true/ false flags that are equivalent to the binary representation of that number! It's a neat trick I found from multiple online forums.

import numpy as np

def dec2bin_bitwise(x):
    'For a 2D NumPy array as input'
    shp = x.shape
    return np.fliplr((x.ravel()[:,None] & (1 << np.arange(8))) > 0)\
        .astype(np.uint8).reshape((*shp, 8))

We have to know the shape of the input array because this approach does create a new axis along which the binary digits are enumerated; for example:

>>> dec2bin_bitwise(np.array((64,)))
array([[0, 1, 0, 0, 0, 0, 0, 0]], dtype=uint8)

The approach above requires an np.fliplr() operation because np.arange() produces a numeric sequence in ascending order, but bit strings are almost all computer systems are ordered from the most-significant bit (at the left) to the least-significant bit. This means that are binary strings are flipped left-to-right. I'm not sure what impact this has on performance compared to simply reversing np.arange(), as below.

import numpy as np

def dec2bin_bitwise2(x):
    'For a 2D NumPy array as input'
    shp = x.shape
    return ((x.ravel()[:,None] & (1 << np.arange(7, -1, -1))) > 0)\
        .astype(np.uint8).reshape((*shp, 8))

An important thing to note about these two functions is that they require arguments that are numpy.ndarray instances, so, they don't strictly work like the example above, with an atomic decimal number, but they are well-suited to the actual problem of working with decimal arrays.

Option 4: NumPy's unpackbits()

I wish I could remember where I first saw this function... It may have been from the NumPy documentation itself (in frustration, desperately seeking a faster solution). This approach does have a stronger assumptions than the previous implementations; specifically, x must be typed unsigned-integer (np.uint8). Also, as in Option 3, this function needs to create a third axis along which the binary digits are enumerated. The axis argument provides some control over this, but in most cases you'd want the new axis to be last (hence, equal to the current number of dimensions, ndim, in Python's number system). Finally, like the first example in Option 3, this function does return a binary string in big-endian order (most significant bit at the end). Thus, it is necessary to reverse-index (flip) the array to get little-endian order

import numpy as np

def dec2bin_unpack(x, axis = None):
    'For an arbitrary NumPy array a input'
    axis = x.ndim if axis is None else axis
    return np.unpackbits(x[...,None], axis = axis)[...,-8:]

Clocking In

For simplicity, in timing each approach, I create a 15-by-15 array, A, of each of the number 0 through 225; the last square matrix I can create using unique decimal numbers smaller than 255. Each function is timed using timeit with 100 loops, the timer repeated 30 times (default). Furthermore, I execute the timeit statement three times and take the average of each trial.

$ python -m timeit -n 100 -r 30 -s "import numpy as np;from dec2bin import dec2bin_numpy, A"
  "dec2bin_numpy(A)"

We can see that it matters a lot which approach you choose! My first implementation, dec2bin_numpy(), was over 40 times slower than the best choice I found. I'm not sure what makes numpy.unpackbits() so fast; I need to look under the hood and report back as, incidentally, the new NumPy documentation makes it harder to find a function's source code.