In Earth system models that run on daily or weekly time steps, there are many quantities that are we may wish to calculate only when the sun is in the sky. Vapor pressure deficit (VPD), as one important example, has strong diurnal variation, tending to decrease in the evening as the ambient temperature declines. As VPD is a key driver of transpiration and photosynthesis [1], if we want to correctly estimate the impact of VPD on these processes, we may need to estimate VPD as it is experienced by plants in the heat of the day. Consequently, we would want to integrate hourly VPD data (such as from a numerical weather model) only for those hours when the sun is up (the photoperiod) and we would therefore need to know the timing of sunrise and sunset.
An alternative approach to such day-length calculations, particularly if we're already integrating data from a weather model, would be to use solar irradiance—an empirical threshold on down-welling short-wave radiation, for instance, would be an acceptable proxy for the sun is in the sky. This is the approach used in photosynthesis models like MODIS MOD17 [2]. However, this empirical threshold might vary between sites and seasons; it's ultimately arbitrary. But the approach is attractive because the calculation of sunrise and sunset times is fairly elaborate. Further, if our model has a large spatial domain—say, continental to global scales—we inevitably need to calculate sunrise and sunset at different latitudes, across different longitudes, and possibly taking into account very different elevations.
I recently ran into this issue when developing a new photosynthesis model in Python. The Python developer community ostensibly has at least two choices of open-source libraries for calculating sunrise and sunset times (I did not look at Skyfield or AstroPy). Both libraries, pyephem and astral, are targeted at more general problems than calculating solar transits on Earth, however. Their generality leads to complexity and this translates to longer execution times when you have a global spatial domain and millions of data cells (pixels). Both libraries do offer greater precision and, in the case of the pyephem library, greater accuracy than the solution I've settled upon, which I describe below. pyephem also corrects for atmospheric refraction and, optionally, elevation effects. However, for determining sunrise and sunset times to the nearest hour, we can get by with less sophistication.
Descriptions of sunrise and sunset calculation on the internet are pretty lacking. NOAA's Earth System Research Laboratories (ESRL) offers a spreadsheet calculator but no details on how it works. This has led some developers to implement a version in code that calculates the value in each column, as in this Matlab example, as if the ESRL calculator was some sacred but indecipherable tome. I wanted to do better, at least in the documentation, verification, and wall time of my own sunrise and sunset calculation. Jean Meeus' "Astronomical Algorithms" [3] provides a calculation, but it relies on ephemeris tables to look-up declination and right ascension. Here, I mostly follow the algorithm described in the U.S. Naval Observatory's Almanac for Computers [4], which a hobbyist named Ed Williams put on their website. I can't find a copy anywhere else, so I'm indebted to them. Both Meeus and the U.S. Naval Observatory describe the calculation in the equatorial coordinate system, in terms of hour angles and the declination of the sun. The approach in Almanac for Computers may be preferable from a standpoint of numeric stability stability, as Meeus' equations require a high number of significant digits in order to be accurate.
Day Length Algorithm Description
Jean Meeus [3] gives the equation for the approximate hour angle of sunrise and sunset:
Where \(H_0\) is the Greenwich hour angle of sunrise (or sunset), i.e., the local hour angle at the prime meridian; \(h_0\) is the zenith angle of the sun; \(\phi\) is the observer's latitude; and \(\delta\) is the declination of the sun.
The general approach to calculating sunrise and sunset times treats the heavens as a clock. Celestial phenomena (including sunrise and sunsets) happen on a schedule, so the positions of celestial bodies, including the sun, can be described by periodic equations that take time as an argument. There are four basic steps to calculating sunrise and sunset times:
- Finding the mean solar time that describes where (or "when") the current moment is in the celestial cycle;
- Calculating the sun's position in the ecliptic coordinate system;
- Converting the sun's ecliptic coordinates to coordinates in the equatorial coordinate system;
- Obtaining the sunrise and sunset times at the Greenwich meridian, then adding or subtracting the offset for our longitude (or "time zone").
The Almanac for Computers algorithm, which I modify, is based on Meeus' equation above. The algorithm walks us through how to calculate \(\delta\) and to convert between hour angles and clock time so as to obtain sunrise and sunset times. The calculations are first performed in the ecliptic coordinate system, where we pretend that sun revolves around the Earth, and then we perform a coordinate transformation to the equatorial coordinate system. According to the U.S. Naval Observatory, the algorithm obtains an accuracy of \(\pm 2\) minutes for any location between \(\pm 65\) degrees latitude. The central weakness of this algorithm is that it uses constants that are estimated for the "latter half of the twentieth century" for the orbital elements (eccentricity, argument of the perihelion) and for converting between sidereal time and Universal Time. Some of these constants we can replace with mathematical models (e.g., VSOP87) like those described by Jean Meeus, but that's totally unnecessary if we simply we wish to obtain the nearest hour of sunrise and sunset.
The procedure described below assumes that all angles are in degrees, not radians. To convert from radians to degrees, multiply by \(180/\pi\); to convert from degrees to radians, multiply by \(\pi/180\). Latitude and longitude should be in decimal degrees; latitude values south of the equator are negative and longitude values west of the prime meridian are negative. I refer to Greenwich mean time and Coordinated Universal Time (UTC) interchangeably.
Calculating the Mean Solar Time
Our approach to calculating sunrise and sunset times uses the mean solar clock—the average motion of the sun in the sky as seen from Earth. Naturally, we begin by figuring out where we are in this solar cycle based on the current date. We often work in hour angles, an angular distance expressed as the number of hours the Earth has rotated since (or must rotate until) the meridian plane (plane containing Earth's axis and the zenith) intersects the point of the body of interest (here, the sun) projected onto the celestial sphere. Essentially, the hour angle quantifies how many hours the Earth must rotate until (or has rotated since) the object is in the same place in the sky again.
Here, the solar hour angle (SHA) quantifies the angle between the sun and the observer expressed as the number of hours difference between solar noon at the observer's location and that of the Greenwich meridian. As the Earth spins on its axis at a rate of about 15 degrees longitude per hour, this calculate is simply longitude, \(\lambda\), divided by 15:
This is basically the offset from Greenwich mean time: the number of hours east or west of the prime meridian (negative values west). We can use the SHA to obtain an approximate time of sunrise and sunset, the mean solar time, expressed as a fraction of a day (e.g., 30.5 is noon on DOY 30). This approximate time is in Greenwich mean time, and so we subtract the SHA from 12h00 as this is the middle of the solar day, which starts at midnight. The Algorithm calculates this separately for sunrise and sunset, but it's easier to calculate the approximate of transit (when the sun is highest in the sky) rather than do twice the work.
\(DOY\) is the number of days since January 1 of that year on the closed interval \([1, 366]\) (on December 31 in leap years, DOY\(=366\)). This can be obtained easily in Python and other programming languages with date string formatting.
Position of the Sun in Ecliptic Coordinates
In order to calculate the sun's declination, we must first calculate the solar mean anomaly and the equation of the center. The solar mean anomaly, \(M\), is best described by first considering the true anomaly; the true anomaly, \(v\), that quantifies the position of the Earth in its elliptical orbit around the sun. If we imagine a line drawn through the points of aphelion and perihelion (farthest and closest points on our orbit), this is the angle between that line and the line connecting us to the sun (the radius vector), measured from perihelion. "It is the angle over which the object moved, as seen from the Sun, since the previous passage through the perihelion" [3]. The solar mean anomaly, then, is the equivalent angle for a circular orbit with the same period as the true object on its elliptical orbit. "The mean anomaly is the angular distance from perihelion which the planet would have moved if it moved around the Sun with a constant angular velocity" [3]. If \(T\) is measured in Julian centuries, instead:
Where mod refers to the modulus function, i.e., the above quantity should be on the interval \((0,360]\).
The Algorithm for Computers provides an approximation that is simpler and no less accurate for transit estimates to the nearest hour, where \(T\) is measured in Julian days:
Note that \(35\,999.0503\) divided by \(36\,525\) (number of days in a Julian century) equals \(0.9856\). In both cases, note that \(M\) is expressed in degrees, not radians.
Using a circular orbit is a simplification that is corrected in the next step, with the equation of the center, which describes the angular difference (\(v - M\)) between the position of the true body (in its elliptical orbit) and the hypothetical body with constant angular velocity (in its circular orbit). This equation can be used in place of Kepler's equation when the eccentricity, \(e\) of the orbit is small, which holds in the case of Earth's orbit [5], \(e = 0.016711\). The equation of the center is often approximated by a Taylor series expansion, with the accuracy of the estimate improving with the number of powers of \(e\) employed. Meeus [3] provides the expansion for the first four terms, which is sufficient for our aim of day-length calculations on Earth with hourly precision:
The above equation gives the angular difference in radians. If we plug in Earth's \(e\), multiply the coefficients by \(180/\pi\), and move \(M\) to the right-hand side, we obtain the approximation for the true anomaly, \(v\), used in the Almanac for Computers [4]:
We then calculate the ecliptic longitude, \(L\), the angular distance of the sun in the plane of the ecliptic, measured from the primary direction (a line pointing from Earth to the sun on the date of the vernal equinox), i.e., in the geocentric coordinate system. This is the first step of calculating the sun's position in the sky.
Where \(\omega \approx 102.937\,348\) is the argument of the perihelion. \(\omega\) can be calculated as: \(\omega = \pi - \Omega\), where \(\pi\) is the longitude of the perihelion and \(\Omega\) is the longitude of the ascending node [6]. I could not find a reference for \(\omega\) in the Earth-sun system so I calculated it by reading \(\pi = 102.937\,348\) from Meeus' (1991) Table 30.A [3] and assuming that \(\Omega = 0\), given that it does not appear in Table 30.A and at the "mean equinox of the date" the Earth is at the ascending node in its orbit around the sun. This may not be the correct interpretation of this calculation (I am not an astronomer), but it does produce the correct value of \(L\), which can also be verified by comparing the value \(180 + 102.937\,348\) to the value used in Almanac for Computers, \(282.634\). The Almanac does provide a time-varying formula of the longitude of perihelion, \(\ell\), that could be used in place of \(180 + \omega\):
Where \(T\) is measured in Julian centuries and \(\ell\) is obtained in degrees.
Position of the Sun in Equatorial Coordinates
So far, we've been working in the ecliptic coordinate system. Now, we want to convert these coordinates (ecliptic longitude and latitude of the sun, the latter assumed to be zero as it is always very small) to an equatorial coordinate system, expressed as right ascension and declination. This is a great introduction to the equatorial (or "celestial") coordinate system, using Earth's geographic coordinate system as an analog.
The declination of the sun, \(\delta\), is obtained:
Where 23.44 degrees is the maximum tilt of Earth's axis [5]. Note that all of these sines should accept arguments in degrees, not radians.
The right ascension of the sun, \(\alpha\), is obtained:
Where, again, we use the obliquity of the Earth (23.44 degrees). Pre-computing this cosine (and the sine of the obliquity, above) can speed things up.
We also need to check to make sure that the right ascension, \(\alpha\), is in the same quadrant as the sun's longitude, \(L\):
Where \(f()\) is the floor function (i.e., round down to the nearest integer).
The sun's local hour angle can now be obtained using Meeus' equation from before. We define \(h_0 \rightarrow 0\) as the zenith of the sun such that \(h_0 = 90^{\circ}\) for solar noon, i.e., "when the sun is at its zenith." Note that Almanac for Computers defines solar zenith differently such that it equals zero at solar noon; consequently, they use \(\mathrm{cos}(h_0)\) in place of \(\mathrm{sin}(h_0)\), below. We might not set \(h_0\) exactly equal to zero (or exactly equal to 90 if following Almanac for Computers) for sunrise or sunset because of the finite width of the sun's disc and the effect of atmospheric refraction. Elevation of the observer might also be considered. Thus, the definition of \(h_0\) will depend on your application. Meeus writes that 34 minutes (\(0.5\bar{6}\) degrees) "is generally adopted for the effect of refraction at the horizon" and that 16 minutes is added as an approximation of radius of the sun (seen from Earth). Hence, Meeus recommends \(h_0 = -0.8\bar{3}\) degrees (the negative sign indicates the center of the body is below the horizon).
Recall that \(\phi\) is the latitude of the observer.
Edge Cases Near the Poles
If we're above the Arctic Circle or below the Antarctic Circle, it's possible that the sun is always up (never sets) or never up (never rises). We can detect these conditions as follows. If \(\mathrm{cos}(H_0) > 1\), the sun never rises at this location on this date. If \(\mathrm{cos}(H_0) < -1\), the sun never sets at this location on this date.
Putting it All Together
We can now calculate the local rise time or local setting time. We do this differently for sunrise (\(m_{\uparrow}\)) and sunset (\(m_{\downarrow}\)): to make sure that \(H_0\) is in the right quadrant, we must add 360 degrees to the rising time. This allows us to obtain the Greenwich apparent sidereal time (GAST) of sunrise or sunset. Note that, below, we are converting both the local hour angle, \(H_0\) and right ascension, \(\alpha\) to hours by dividing by 15 degrees. The sum of \(H_0\) and \(\alpha*\), both in hours, gives the GAST. We convert from GAST to the local apparent sidereal time by adding the solar hour angle (SHA). Then, we convert from sidereal time to Universal Time (for our purposes, equivalent UTC) for a sunrise (\(1/4\) of a day earlier than the transit) or sunset (\(1/4\) of a day later).
Because \(T\) is the transit time at the Greenwich meridian, as a fraction of the day, we want to subtract \(1/4\) of a day when calculating sunrise and add \(1/4\) of a day when calculating sunset. The scale factor \(0\rlap{.}^{\mathrm{h}}06571\) and offset \(6\rlap{.}^{\mathrm{h}}622\) are in units of hours and are essentially magic numbers.
Note that the sunrise time, \(m_{\uparrow}\), or sunset time \(m_{\downarrow}\) calculated above may not lie on the interval \([0,24)\) and in that case you must add or subtract 24.
Calculating Photoperiod
Although the pyephem implementation (see later in the article) is slow, I take it to be the most accurate source for sunrise and sunset calculation and, hence, photoperiod calculation. I therefore wanted to compare my photoperiod calculation to what pyephem comes up with. I calculated sunrise and sunset hours with both approaches for a latitude-longitude grid, with steps of 5/8° longitude and 1/2° latitude. This is the grid used by the NASA GMAO Modern-Era Retrospective Re-analysis dataset, version 2 (MERRA-2). You can make a pretty picture of photoperiod for the entire globe! For example, on June 25, 2012, global photoperiod kind of looks like this, from short days (darker colors) to longer days (lighter colors):
Below, I visualize the difference between my approach and pyephem; differences are within 2 hours, with pyephem describing slightly shorter days (by 1 hour, shown in blue, or by 2 hours, shown in red) relative to my implementation. Where day length appears to differ by 2 hours, this is only due to a 1-hour rounding difference in both the sunrise and sunset hours. The bias in the direction of shorter days is just because of the offset of the photoperiod calculations and my reduction in precision by rounding both down to the nearest hour. Overall, they agree pretty well.
Python Implementation
I implemented the day-length algorithm described above in Cython—partly because I wanted the practice writing Cython extension modules for Python projects, but also because my experience with pyephem pointed to the need for better performance. A pure-Python implementation can be obtained simply by removing the lines that begin with cdef. Also, I'm rounding down to the nearest hour because I merely need to determine which hours to select from a re-analysis dataset.
I also had to make a decision about how to calculate photoperiod near the poles when the sun is always above or below the horizon. For the austral and boreal summers (sun is always up), I simply decided that the photoperiod must be 24 hours long. Therefore, in the implementation below, I set the sunrise hour to zero and the sunset hour to 23 (Python starts counting at zero). For the austral and boreal winters (sun is always down), however, the solution is not obvious.
For a model that needs to make daily calculations everywhere on the Earth, it seems that even if the sun never rises we need to calculate a daily temperature, daily VPD, et cetera. These are mean quantities over any number of hours, so it doesn't matter how long the day is as long as we have at least one data point to average. Therefore, even when the sun is always below the horizon, I decided that "photoperiod" should also be 24 hours long (same as when the sun is always up). For a photosynthesis model, GPP is likely very close to zero under these conditions, so it doesn't matter much. For other applications, you may want to determine photoperiod during the winter differently. In my implementation below, I emit -1 for the sunrise and sunset hours if the sun is always below the horizon so that we can decided what to do later.
import datetime
import numpy as np
cdef list coords
cdef int doy
cdef float x, zenith, lat, lng, lng_hour, tmean, anomaly
cdef float lng_sun, ra, ra_hours, dec_sin, dec_cos
cdef float hour_angle_cos, hour_angle, hour_rise, hour_sets
# The sunrise_sunset() algorithm was written for degrees, not radians
sine = lambda x: np.sin(np.deg2rad(x))
cosine = lambda x: np.cos(np.deg2rad(x))
tan = lambda x: np.tan(np.deg2rad(x))
arcsin = lambda x: np.rad2deg(np.arcsin(x))
arccos = lambda x: np.rad2deg(np.arccos(x))
arctan = lambda x: np.rad2deg(np.arctan(x))
def sunrise_sunset(coords, dt, zenith = -0.83):
'''
Returns the hour of sunrise and sunset for a given date. Hours are on the
closed interval [0, 23] because Python starts counting at zero; i.e., if
we want to index an array of hourly data, 23 is the last hour of the day.
Recommended solar zenith angles for sunrise and sunset are -6 degrees for
civil sunrise/ sunset; -0.5 degrees for "official" sunrise/sunset; and
-0.83 degrees to account for the effects of refraction. A zenith angle of
-0.5 degrees produces results closest to those of pyephem's
Observer.next_rising() and Observer.next_setting(). This calculation does
not include corrections for elevation or nutation nor does it explicitly
correct for atmospheric refraction. Source:
U.S. Naval Observatory. "Almanac for Computers." 1990.
Parameters
----------
coords : list or tuple
The (longitude, latitude) coordinates of interest; coordinates can
be scalars or arrays (for times at multiple locations on same date)
dt : datetime.date
The date on which sunrise and sunset times are desired
zenith : float
The sun zenith angle to use in calculation, i.e., the angle of the
sun with respect to its highest point in the sky (90 is solar noon)
(Default: -0.83)
Returns
-------
tuple
2-element tuple of (sunrise hour, sunset hour)
'''
lat, lng = coords
assert -90 <= lat <= 90, 'Latitude error'
assert -180 <= lng <= 180, 'Longitude error'
doy = int(dt.strftime('%j'))
# Calculate longitude hour (Earth turns 15 degrees longitude per hour)
lng_hour = lng / 15.0
# Appoximate transit time (longitudinal average)
tmean = doy + ((12 - lng_hour) / 24)
# Solar mean anomaly at rising, setting time
anomaly = (0.98560028 * tmean) - 3.289
# Calculate sun's true longitude by calculating the true anomaly
# (anomaly + equation of the center), then add (180 + omega)
# where omega = 102.634 is the longitude of the perihelion
lng_sun = (anomaly + (1.916 * sine(anomaly)) +\
(0.02 * sine(2 * anomaly)) + 282.634) % 360
# Sun's right ascension (by 0.91747 = cosine of Earth's obliquity)
ra = arctan(0.91747 * tan(lng_sun)) % 360
# Adjust RA to be in the same quadrant as the sun's true longitude, then
# convert to hours by dividing by 15 degrees
ra += np.subtract(
np.floor(lng_sun / 90) * 90, np.floor(ra / 90) * 90)
ra_hours = ra / 15
# Sun's declination's (using 0.39782 = sine of Earth's obliquity)
# retained as sine and cosine
dec_sin = 0.39782 * sine(lng_sun)
dec_cos = cosine(arcsin(dec_sin))
# Cosine of the sun's local hour angle
hour_angle_cos = (
sine(zenith) - (dec_sin * sine(lat))) / (dec_cos * cosine(lat))
# Correct for polar summer or winter, i.e., when the sun is always
# above or below the horizon
if hour_angle_cos > 1 or hour_angle_cos < -1:
if hour_angle_cos > 1:
return (0, 0) # Sun is always down
elif hour_angle_cos < -1:
return (0, 23) # Sun is always up
hour_angle = arccos(hour_angle_cos)
# Local mean time of rising or setting (converting hour angle to hours)
hour_rise = ((360 - hour_angle) / 15) + ra_hours -\
(0.06571 * (tmean - 0.25)) - 6.622
hour_sets = (hour_angle / 15) + ra_hours -\
(0.06571 * (tmean + 0.25)) - 6.622
# Round to nearest hour, convert to UTC
return (
np.floor((hour_rise - lng_hour) % 24),
np.floor((hour_sets - lng_hour) % 24))
Should we always round down to the nearest hour? Or should we round to the nearest whole hour (round, not floor), possibly rounding up? I find that rounding down (floor) produces evenly spaced photoperiod bands across longitudes. Any other rounding scheme produces a kind of aliasing that biases day length high or low at a certain longitude. Again, you should decide what is best for your application.
Using Photoperiod for Climatic Data Aggregation
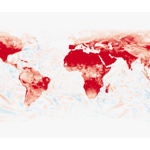
What impact does a sun-up calculation of climatic variables have? Specifically, compared to a simple daily average over 24 hours, do we see an impact from an average calculated only over the photoperiod? If we look at the difference in VPD (on June 25, 2012) between a 24-hour calculation and a photoperiod calculation, we see that the atmospheric moisture demand over land is much higher when it is aggregated from hourly data when the sun is up. This makes sense—it's hotter during the day—but the sun-up calculation of VPD might also more accurately represent the atmospheric moisture demand experienced by plants during photosynthesis. The difference can be as much 700 Pa! (I clipped the image below to 600 Pa for better visualization.)
Note that while there is a faint stamping pattern of the photoperiod on the above difference image, the daylight-aggregated VPD image does not show these artifacts.
Competing Approaches
Before describing the pyephem and astral approaches, I want to further motivate my work here. I timed the pyephem and astral implementations (code below) using Python's timeit module. The wall times below (in microseconds) are the average of the per-loop times in three trials under similar CPU loads, for an Intel Core i7-10710U (1.10 GHz) CPU.
$ python -m timeit -n 100 -s "import datetime;from my_module import updown_func"
"updown_func((42, -83), datetime.datetime.today())"
| Implementation | Time (usec) |
|---|---|
pyephem |
544 |
astral |
125 |
| Almanac for Computers (Python) | 75 |
| My algorithm (Cython) | 63 |
The Cython implementation is the one I showed above. The Almanac for Computers (Python) implementation is similar but is in pure Python and calculates separate quantities throughout for sunrise and sunset—literally the way it is described in the Almanac, but ultimately unnecessary. The speed-up between the Python and Cython versions is probably due to the static typing of Cython, not that we discarded some redundant calculations.
The pyephem approach asks us to define an observer and a celestial body (in this case, the sun). I like their API, especially the custom error classes AlwaysUpError and NeverUpError. As with the Almanac for Computers implementation, dt is a datetime.date instance and coords is a 2-element sequence of latitude and longitude.
import ephem
SUN = ephem.Sun() # Module-level constant
obs = ephem.Observer()
# Positions in degrees are expected to be str type
obs.lat, obs.long = map(str, coords)
obs.date = dt.strftime('%Y-%m-%d')
obs.pressure = 0 # Do not calculate refraction
try:
rising = obs.next_rising(SUN).datetime().hour
except (ephem.AlwaysUpError, ephem.NeverUpError):
rising = -1
try:
setting = obs.next_setting(SUN).datetime().hour
except ephem.AlwaysUpError:
setting = 23
except ephem.NeverUpError:
setting = -1
return (rising, setting)
In the astral implementation, we don't have custom error classes differentiating cases where the sun is always above or below the horizon. There is a ValueError issued when one tries to observe the sun from north of (south of) the Arctic (Antarctic) Circle. Therefore, I had to implement a pretty poor hack; we check to see if we're above or below the Arctic or Antarctic circles, respectively, in the summer or winter.
from astral import LocationInfo
from astral.sun import sun
lat, lng = coords
loc = LocationInfo()
loc.latitude = lat
loc.longitude = lng
try:
s = sun(loc.observer, date = dt)
except ValueError as err:
if lat > 60 and dt.month in (4, 5, 6, 7, 8, 9):
return (0, 23) # Sun always up above Arctic Circle
if lat < -60 and dt.month in (1, 2, 3, 10, 11, 12):
return (0, 23) # Sun always up below Antarctic Circle
return (-1, -1) # Sun always down
return (s['sunrise'].hour, s['sunset'].hour)
I can't recommend the astral implementation, above, because of this hack. But why is the pyephem approach so slow? The backbone of pyephem is implemented in C, but there may be some overhead in initialization of the Observer(). If you only need to calculate transit times for a single observer-body pair, this performance hit would go unnoticed. However, if you need to calculate transit times for all the pixels in a global Earth system model, I think the modified Almanac approach is the best choice.
References
- Chapin, F. S., Matson, P. A., & Vitousek, P. M. (2011). Principles of Terrestrial Ecosystem Ecology. Springer New York.
- Zhao, M., Heinsch, F. A., Nemani, R. R., & Running, S. W. (2005). Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sensing of Environment, 95, 164–176.
- Meeus, J. (1991). Astronomical Algorithms. Willman-Bell Inc.
- U.S. Naval Observatory. (1990). Almanac for Computers. The Nautical Almanac Office, U.S. Naval Observatory, Washington, D.C.
- NASA (2021). "Earth Fact Sheet." Accessed: February 10, 2021.
- Andøya Space Center (2021). "Introduction of the six basic parameters describing satellite orbits." Accessed: February 10, 2021.